5年ほど前、このブログで虚数のテトレーションという記事を書いたことがある。テトレーション(tetration)とは、自らのべき乗を指定された回数反復する演算のことで、na と表現する。35 の場合、555 = 1.911×102185 となる。Pythonの関数で表現すれば以下のようになる。
以前の記事では、∞i が 0.43828+0.36059i に収束することを見つけたのだが、今回はそれに関連したフラクタルについて紹介したい。
テトレーション na の a には複素数を指定することができる。このとき、a = x + yi として、それを複素平面に置く。ここで正の整数nを大きくしていき、発散と判定されたnに対応した色で平面を色分けする。発散しない場合、予め決めておいたnの上限値を使う。これで得られる図をテトレーション・フラクタル(tetration fractal)と呼ぶ。
n(x + yi)=a + biとしたとき、n+1(x + yi)=a' + b'i は以下のように計算できる。
Pythonでの実装はActiveSate CodeにTetration Fractalとして載っている。今回はこれを少し修正したコード、C++で書いたコード、更にTBBで並列化したコードを用意して、それらの実行速度のベンチマークを取ってみた。
ここで、複素平面の領域は(-1.5, 0)-(-0.75, 0.75)であり、最大繰り返し数は256としている。画像の大きさは1,024×1,024とした。実行環境はIntel Xeon X5650の2CPUで、12コア・24スレッドとなっている。
以下に、ソースコードを示す。詳細についてはコードを読んでいただきたい。
Pythonによる実装:
% ./tetration.py tetration.png -1.5 0.0 0.75 0.75 1024 1024
C++による実装:
% g++ tetration.cpp -o tetration -O3
% ./tetration tetration.out -1.5 0.0 0.75 0.75 1024 1024
% ./image_tetration.py tetration.out tetration.png
TBBを利用したC++による並列化実装:
% g++ tetration_tbb.cpp -o tetration_tbb -ltbb -O3
% ./tetration_tbb tetration.out -1.5 0.0 0.75 0.75 1024 1024
% ./image_tetration.py tetration.out tetration.png
C++の実行ファイルで生成された出力ファイルを画像ファイルに変換するスクリプトを以下に示す。
以前の記事では、∞i が 0.43828+0.36059i に収束することを見つけたのだが、今回はそれに関連したフラクタルについて紹介したい。
テトレーション na の a には複素数を指定することができる。このとき、a = x + yi として、それを複素平面に置く。ここで正の整数nを大きくしていき、発散と判定されたnに対応した色で平面を色分けする。発散しない場合、予め決めておいたnの上限値を使う。これで得られる図をテトレーション・フラクタル(tetration fractal)と呼ぶ。
n(x + yi)=a + biとしたとき、n+1(x + yi)=a' + b'i は以下のように計算できる。
Pythonでの実装はActiveSate CodeにTetration Fractalとして載っている。今回はこれを少し修正したコード、C++で書いたコード、更にTBBで並列化したコードを用意して、それらの実行速度のベンチマークを取ってみた。
| Python | C++ | C++ with TBB |
| 258.732秒 | 16.999秒 | 0.976秒 |
ここで、複素平面の領域は(-1.5, 0)-(-0.75, 0.75)であり、最大繰り返し数は256としている。画像の大きさは1,024×1,024とした。実行環境はIntel Xeon X5650の2CPUで、12コア・24スレッドとなっている。
以下に、ソースコードを示す。詳細についてはコードを読んでいただきたい。
Pythonによる実装:
% ./tetration.py tetration.png -1.5 0.0 0.75 0.75 1024 1024
C++による実装:
% g++ tetration.cpp -o tetration -O3
% ./tetration tetration.out -1.5 0.0 0.75 0.75 1024 1024
% ./image_tetration.py tetration.out tetration.png
TBBを利用したC++による並列化実装:
% g++ tetration_tbb.cpp -o tetration_tbb -ltbb -O3
% ./tetration_tbb tetration.out -1.5 0.0 0.75 0.75 1024 1024
% ./image_tetration.py tetration.out tetration.png
C++の実行ファイルで生成された出力ファイルを画像ファイルに変換するスクリプトを以下に示す。

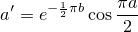
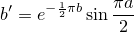
コメント
Cython を使うと、 C++ のコードと同程度の速度で計算が行なえました。手軽なので試す価値はあるように思います。
CythonはPythonの高速化の他にも、Cへのラッパーとしても使えて便利ですね。
NumPyモジュールとの組み合わせなども有用だと思います。